| Vorheriges Thema anzeigen :: Nächstes Thema anzeigen |
| Autor |
Nachricht |
Backside
NGC 2997

Anmeldungsdatum: 17.07.2003
Beiträge: 755
Wohnort: Sirius
|
 (#162061) Verfasst am: 05.08.2004, 23:15 Titel: Lagrange-Punkte (#162061) Verfasst am: 05.08.2004, 23:15 Titel: Lagrange-Punkte |
 |
|
Nabend!
Ich hätte da mal eine Frage zu den Lagrange-Punkten.
Diese sind ja bekannt als folgendes :
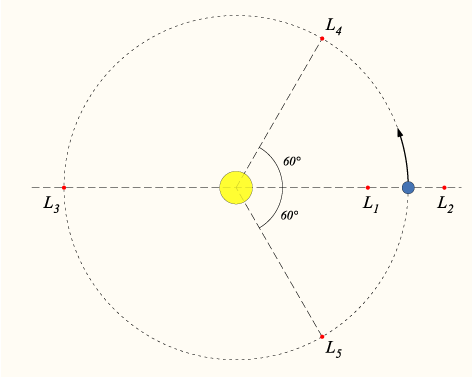
Kurze Erläuterung:
Die Lagrange-Punkte sind Punkte, an denen sich dritte Körper aufhalten können, ohne von den gravitativen Wirkungen der beiden anderen (z.B. hier Sonne und Erde) großartig gestört zu werden.
Man spricht auch von "stabilität".
D.h. ein Körper in einem dieser Punkte bleibt dort bezüglich der anderen beiden stationär, ohne dass man dafür Energie aufwenden müsste (vorausgesetzt, der Körper umkreist (in diesem Beispiel) die Sonne mit der gleichen Geschwindigkeit und Richtung wie die Erde).
Allerdings habe ich damit so meine Probleme, denn die Eigenschaft dieser Punkte ist ja gerade die, dass ein Körper dort nicht von den anderen Beiden abgelenkt bzw. angezogen wird.
Doch genau das ist doch eigentlich ausschließlich im Punkt L1 möglich, da sich dort die Kräfte von Sonne und Erde aufheben.
L2 und L3 lasse ich mir unter Berücksichtigung der Bedingung, dass die Erde um die Sonne kreist, vielleicht noch eingehen, denn ich vermute es handelt sich um einen "Fliekraft"-ähnlichen Effekt wie z.B. bei dem mondabgewandten Flutberg auf der Erde.
Doch wie bitte kommt es zu L4 und L5 ? Ein Körper dort steht in jedem Fall im gravitativen Einfluss von Sonne und Erde, sollten also eigentlich von diesen angezogen werden!
Warum bleiben Körper in diesen Punkten aber so stabil ?
Ich habe im Netz nichts dazu gefunden, vielleicht kann einer von euch Freaks mir weiterhelfen ?
Ich weis, dass die Berechnungen dazu mehrere Seiten umfassen (zumindest hat Lagrange mehrere Seiten gebraucht) und will daher also nicht (unbedingt  ) wissen, wie man das berechnet. ) wissen, wie man das berechnet.
Es würde mir schon reichen, wenn mir jemand sagen könnte, welche Effekte wie dafür verantwortlich sind, dass sich ein Körper in z.B. L5 nicht in Richtung Sonne|Erde zubewegt, sondern stationär bleibt.
Greetings, Backside
_________________
Atheist = Realist
|
|
| Nach oben |
|
 |
Reichsbedenkenträger
wechselhaft

Anmeldungsdatum: 13.07.2004
Beiträge: 1089
Wohnort: S-H
|
 (#162110) Verfasst am: 06.08.2004, 00:02 Titel: (#162110) Verfasst am: 06.08.2004, 00:02 Titel: |
 |
|
  

Teufelswerk
_________________
Wer nach allen Seiten offen ist, kann nicht ganz dicht sein.
|
|
| Nach oben |
|
 |
frajo
dauerhaft gesperrt
Anmeldungsdatum: 25.08.2003
Beiträge: 11440
|
 (#162137) Verfasst am: 06.08.2004, 00:46 Titel: (#162137) Verfasst am: 06.08.2004, 00:46 Titel: |
 |
|
ich fürchte, hier gibt es nicht viel zu "verstehen" im sinne von "plausibel machen".
wir haben es hier nun mal mit einem spezialfall des allgemeinen drei-körper-problems zu tun. während das allgemeine problem nicht analytisch lösbar ist, gibt es in eben diesem spezialfall mit den lagrange-punkten ausnahmsweise doch eine analytische lösung. und die sagt halt aus, daß die punkte L<sub>1</sub> ... L<sub>5</sub> insofern ausgezeichnete punkte sind, als sich an diesen orten ein massepunkt aufhalten kann, ohne die kinematik des gesamtsystems (aus drei massepunkten) zu beeinträchtigen. 
|
|
| Nach oben |
|
 |
step
registriert

Anmeldungsdatum: 17.07.2003
Beiträge: 22782
Wohnort: Germering
|
 (#162891) Verfasst am: 07.08.2004, 14:13 Titel: (#162891) Verfasst am: 07.08.2004, 14:13 Titel: |
 |
|
Hi Backside,
L4 und L5 sind im Gegensatz zu den anderen L-Punkten leicht stabil, in der Natur kommen also tatsächlich Massen an solchen Stellen vor, z.B. die "Trojaner" im System Sonne / Jupiter.
Dein Verständnisproblem beruht vermutlich auf einem oder mehreren der folgenden Punkte:
- zwar wirken auf L4 und L5 nur die gravitativen Kräfte der zwei Hauptkörper, aber sie wirken als Beschleunigung, d.h. sie "ziehen am momentanen Geschwindigkeitsvektor". Wenn dieser nicht null ist - wenn also L4 bzgl. des Systems nicht ruht, resultiert das in einer leichten Ablenkung der Flugbahn und letztlich in einer Kreis- oder elliptischen Bahn - ebenso wie ja die Erde nicht einfach in die Sonne fällt, sondern immer an ihr vorbei. Die Punkte L4 und L5 können natürlich nur deshalb stabil sein, weil sie auf der gleichen Bahn voraus- bzw. hinterherlaufen - in immer gleichem Abstand. L4 und L5 gibt es also nur in einem rotierenden System.
- das ganze gilt nur, wenn die Massen an L4 und L5 vernachlässigbar klein sind, denn sonst würden sie selbst das System Sonne/Erde destabilisieren. Genaugenommen gilt es übrigens nur, wenn die Zentralmasse selbst wiederum wesentlich schwerer als die zweite Hauptmasse ist.
Deine Idee, Scheinkräfte zuhilfezunehmen, ist gar nicht so schlecht. In der Tat rechnet man dies - jedenfalls in der klassischen Mechanik - meist mithilfe der Fliehkraft und einem entsprechenden Effektivpotential:

Auch sonst ganz kurz und gut:
http://www.lutz-peter.hoogi.de/physik/lagrange/lagrange.html
Schön durchgerechnet, auch mit Stabilitätsanalyse in Abhängigkeit von den Hauptmassen, ist es hier:
http://map.gsfc.nasa.gov/ContentMedia/lagrange.pdf
gruß/step
_________________
Was ist der Sinn des Lebens? - Keiner, aber Leere ist Fülle für den, der sie sieht.
|
|
| Nach oben |
|
 |
Backside
NGC 2997

Anmeldungsdatum: 17.07.2003
Beiträge: 755
Wohnort: Sirius
|
 (#168166) Verfasst am: 21.08.2004, 14:38 Titel: (#168166) Verfasst am: 21.08.2004, 14:38 Titel: |
 |
|
Hi step,
danke für die Antwort, sie ist auf jeden Fall die Lösung für mein Problem!
Mir ist zwar jetzt klargeworden, warum gerade ein gleichseitiges Dreieck damit was zu tun hat, allerdings ist dennoch irgendwas faul mit folgender Formel:

Nach der von dir geposteten Seite interpretiere ich r als Vektor, der vom Sonnenmittelpunkt aus auf einen beliebigen Punkt (x, y) zeigt (also einfach zweidimensional betrachtet).
R ist ja der Abstand Sonne-Erde und M = m1 + m2
Setzt man für (x, y) die Koordinaten von z.B. L4 ein (wobei die Sonne im Koordinatenursprung liegen soll, wodurch r1 = 0 ist), so müsste in der großen Klammer eigentlich Null herauskommen ... tut es aber nicht ... oder doch ?
Setze ich jedenfalls L4: r := (x, y) = R*(0.5, SQR(3)/2) (wobei die Erde die Koordinaten (R, 0) hat), dann erhalte ich:
m1*-r/R³ + m2*(0.5, -SQR(3)/2)/R³ -(m1+m2)/R³*r
1/R³ klammer ich aus und der Klammerinhalt ist mit r vollständig eingesetzt:
m1*(-0.5, -SQR(3)/2) + m2*(0.5, -SQR(3)/2) + m1*(-0.5, -SQR(3)/2) + m2*(-0.5, -SQR(3)/2)
= m1*(-1, -SQR(3)) + m2*(0, -SQR(3))
und das ist alles andere als Null!
Wo steckt bitte der Fehler ?
MfG, Backside
_________________
Atheist = Realist
|
|
| Nach oben |
|
 |
step
registriert

Anmeldungsdatum: 17.07.2003
Beiträge: 22782
Wohnort: Germering
|
 (#168185) Verfasst am: 21.08.2004, 15:28 Titel: (#168185) Verfasst am: 21.08.2004, 15:28 Titel: |
 |
|
| Backside hat folgendes geschrieben: | | Wo steckt bitte der Fehler ? |
Es ist nicht besonders günstig, den Ursprung in den Sonnenmittelpunkt zu legen .... und zudem bist Du Deiner eigenen ungenauen (um nicht zu sagen falschen) Zeichnung aufgesessen.
Wenn Du den Ursprung in den Schwerpunkt von M1 und M2 legst, und das richtige Ergebnis
x = R/2 * (M1-M2)/(M1+M2)
y = sqrt(3)/2
einsetzt, sollte es funktionieren.
Wenn Du in den Lösungen übrigens M2 gegenüber M1 vernachlässigst, und nur dann, erhätst Du das gleichseitige Dreieick mit einer Ecke im Sonnenmittelpunkt, das Du fälschlicherweise bereits vorausgesetzt hast.
gruß/step
_________________
Was ist der Sinn des Lebens? - Keiner, aber Leere ist Fülle für den, der sie sieht.
|
|
| Nach oben |
|
 |
|

