| Vorheriges Thema anzeigen :: Nächstes Thema anzeigen |
| Autor |
Nachricht |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1811930) Verfasst am: 29.01.2013, 14:15 Titel: Fragen zur Quantenmechanik (#1811930) Verfasst am: 29.01.2013, 14:15 Titel: Fragen zur Quantenmechanik |
 |
|
Hallo liebes Forum!
Ich studiere eigentlich Philosophie und interessiere mich sehr für Naturphilsophie und in diesem Zusammenhang natürlich auch sehr für die Quantenmechanik. Da ich schon öfter den Vorwurf von Physikern gehört habe, Philosophen labern nur über die Quantenphysik und kennen sich eigentlich gar nicht damit aus (vllt nicht völlig zu Unrecht  ), versuche ich jetzt ein bisschen nachzulernen. ), versuche ich jetzt ein bisschen nachzulernen.
Dabei sind mir folgende Fragen gekommen und wollte fragen, ob ihr mir da weiterhelfen könnt.
1.) Wenn eine Wellenfunktion psi in L^2 und daher normalisierbar ist, folgt daraus dann
lim psi(x)=0 (für x->unendlich)?
Irgendwie habe ich das Gefühl, es müsste schon so sein, weiß aber nicht sicher, wie man dafür argumentiert.
2.) Quantenmechanik lebt ja auf dem Hilbertraum L^2. Wie kann man es vereinbaren, dass nicht jede Funktion in L^2 differenzierbar ist, wir aber gleichzeitig mit dem Laplace-Operator arbeiten?
Vielen Dank, vielleicht fallen mir bald noch neue Fragen ein.
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
sponor
registrierter User

Anmeldungsdatum: 16.05.2008
Beiträge: 1712
Wohnort: München
|
 (#1811967) Verfasst am: 29.01.2013, 16:03 Titel: (#1811967) Verfasst am: 29.01.2013, 16:03 Titel: |
 |
|
Hallo und willkommen!
Zu 1: Für eine Funktion folgt das m.W. nicht – man kann wohl "pathologische" Funktionen definieren, die zwar quadratintegrabel sind, aber trotzdem nicht verschwinden.
Für eine Wellenfunktion (von gebundenen Zuständen) gilt es aber schon – per Definition. (Ich glaube, das läuft auf die Erhaltung der Materie hinaus.)
Zu 2: Verstehe das Problem nicht ganz... Auch hier muss man halt geeignete Definition wählen: Nicht jede L2-Funktion kann/darf auch eine Wellenfunktion sein.
(Das ist in der Physik eigentlich überall so, die Definitionsbereichsangabe wird aber gern vergessen.  Genauso, wie man oft "unphysikalische" Ergebnisse verwirft, negative Terme oder so.) Genauso, wie man oft "unphysikalische" Ergebnisse verwirft, negative Terme oder so.)
_________________
Unsere Welt wird noch so fein werden, daß es so lächerlich sein wird, einen Gott zu glauben als heutzutage Gespenster.
(G. Chr. Lichtenberg)
|
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1811984) Verfasst am: 29.01.2013, 16:51 Titel: (#1811984) Verfasst am: 29.01.2013, 16:51 Titel: |
 |
|
Vielen Dank für Deine Antwort.
Zu 1.) Ja, immer diese Mathematiker mit ihren pathologischen Gegenbeispielen  Ich werde mal das Netz durchforsten, um ein solches zu finden. Ich werde mal das Netz durchforsten, um ein solches zu finden.
Zu 2.) Also ist der L^2 strenggenommen gar nicht der Hilbertraum, auf dem Quantenmechanik betrieben wird, sondern der Schnitt von L^2 mit dem Raum der 2-fach differenzierbaren Funktionen?
Gibt es (interessante) quantenechanische Systeme ohne Laplace-operator, d.h. ohne kinetische Energie?
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
step
registriert

Anmeldungsdatum: 17.07.2003
Beiträge: 22782
Wohnort: Germering
|
 (#1811986) Verfasst am: 29.01.2013, 16:53 Titel: Re: Fragen zur Quantenmechanik (#1811986) Verfasst am: 29.01.2013, 16:53 Titel: Re: Fragen zur Quantenmechanik |
 |
|
@petringer: Das sind sehr gute Fragen! (für einen Philosophen 
| petringer hat folgendes geschrieben: | | 1.) Wenn eine Wellenfunktion psi in L^2 und daher normalisierbar ist, folgt daraus dann lim psi(x)=0 (für x->unendlich)? Irgendwie habe ich das Gefühl, es müsste schon so sein, weiß aber nicht sicher, wie man dafür argumentiert. |
Dazu wollte ich noch was gutes raussuchen, was ich mal dazu gelesen habe, muß Dich aber auf später vertrösten.
| petringer hat folgendes geschrieben: | | 2.) Quantenmechanik lebt ja auf dem Hilbertraum L^2. Wie kann man es vereinbaren, dass nicht jede Funktion in L^2 differenzierbar ist, wir aber gleichzeitig mit dem Laplace-Operator arbeiten? |
Hat sponor schon gut beantwortet. Ich würde vielleicht ergänzen, daß wir in der (üblichen) Quantenmechanik ja nur Wellenfunktionen betrachten, die Lösungen bestimmter Differentialgleichungen, zum Beispiel der Schrödingergleichung, sind.
_________________
Was ist der Sinn des Lebens? - Keiner, aber Leere ist Fülle für den, der sie sieht.
|
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1812088) Verfasst am: 29.01.2013, 20:32 Titel: (#1812088) Verfasst am: 29.01.2013, 20:32 Titel: |
 |
|
Ich habe jetzt ein Gegenbeispiel für meine ursprüngliche Behauptung gefunden. Man muss einfach nur eine Funktion nehmen, die bei jeder natürlichen Zahl n auf eins geht, der Höcker darf aber nicht breiter als 1/n^2 sein. Dann kann man das Integral mit Summe(1/n^2)=pi^2/6 dominieren.
Was das jetzt physikalisch für einen Sinn hat, weiß ich aber auch nicht.
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
Tso Wang
Vergiß es

Anmeldungsdatum: 21.09.2003
Beiträge: 1433
|
 (#1812132) Verfasst am: 29.01.2013, 21:41 Titel: Re: Fragen zur Quantenmechanik (#1812132) Verfasst am: 29.01.2013, 21:41 Titel: Re: Fragen zur Quantenmechanik |
 |
|
| step hat folgendes geschrieben: | @petringer: Das sind sehr gute Fragen! (für einen Philosophen 
| petringer hat folgendes geschrieben: | | 1.) Wenn eine Wellenfunktion psi in L^2 und daher normalisierbar ist, folgt daraus dann lim psi(x)=0 (für x->unendlich)? Irgendwie habe ich das Gefühl, es müsste schon so sein, weiß aber nicht sicher, wie man dafür argumentiert. |
Dazu wollte ich noch was gutes raussuchen, was ich mal dazu gelesen habe, muß Dich aber auf später vertrösten.
|
.
Ich mag mich irren, aber müsste das von der Argumentation her nicht darauf hinauslaufen, daß die Wahrscheinlichkeit ein Teilchen anzutreffen gegen Null geht, wenn der "Raum" unendlich groß wird ? Oder bringe da gerade etwas durcheinander ?
()
_________________
Geh' weiter
|
|
| Nach oben |
|
 |
step
registriert

Anmeldungsdatum: 17.07.2003
Beiträge: 22782
Wohnort: Germering
|
 (#1812138) Verfasst am: 29.01.2013, 22:01 Titel: Re: Fragen zur Quantenmechanik (#1812138) Verfasst am: 29.01.2013, 22:01 Titel: Re: Fragen zur Quantenmechanik |
 |
|
| step hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | 1.) Wenn eine Wellenfunktion psi in L^2 und daher normalisierbar ist, folgt daraus dann lim psi(x)=0 (für x->unendlich)? Irgendwie habe ich das Gefühl, es müsste schon so sein, weiß aber nicht sicher, wie man dafür argumentiert. |
Dazu wollte ich noch was gutes raussuchen, was ich mal dazu gelesen habe, muß Dich aber auf später vertrösten. |
Leider nicht gefunden. Also ohne: Der lim=0 gilt meines Erachtens nur für bestimmte zeitunabhängige Lösungen - etwa Potentiale, die nach außen sehr hoch werden. Meistens führt dabei der Potenzialterm in der Differentialgleichung zu Lösungen mit e^(-x) o.ä. Verhalten.
Betrachtet man dagegen die allgemeine zeitabhängige Schrödingergleichung oder auch die Quantenfeldtheorien, so erlauben diese durchaus Lösungen, die im (Raumzeit-) Unendlichen nicht generell verschwinden.
Einfachstes Beispiel ist eine ebene elektromagnetische Welle e^(ik(x,t)), aka Photon im Vakuum.
Hier wird es mit der Gesamt-Aufenthaltswahrscheinlichkeit etwas knifflig, da sie im Wellenbild überall gleich ist (wegen des fixen Impulses). Geht man ins Teilchenbild, erhält man eine Überlagerung mehrerer Wellen und eine Gesamtwelle, die nach außen wieder lim=0 hat.
_________________
Was ist der Sinn des Lebens? - Keiner, aber Leere ist Fülle für den, der sie sieht.
|
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1812152) Verfasst am: 29.01.2013, 23:02 Titel: (#1812152) Verfasst am: 29.01.2013, 23:02 Titel: |
 |
|
Ich hätte ja jetzt schon ein (pathologisches) Gegenbeispiel (s.o.).
Die ebene Welle hat doch das Problem, nicht in L^2 zu sein. Wie rechtfertigt man dann, dass k^2 im Energiespektrum ist, da doch
-L (exp(-ikx))=k^2 (exp(-ikx)) ,wobei
L der Laplaceoperator ist und ich diese ganzen nervigen Konstanten weggelassen habe?
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
step
registriert

Anmeldungsdatum: 17.07.2003
Beiträge: 22782
Wohnort: Germering
|
 (#1812156) Verfasst am: 29.01.2013, 23:25 Titel: (#1812156) Verfasst am: 29.01.2013, 23:25 Titel: |
 |
|
| petringer hat folgendes geschrieben: | Die ebene Welle hat doch das Problem, nicht in L^2 zu sein. Wie rechtfertigt man dann, dass k^2 im Energiespektrum ist, da doch
-L (exp(-ikx))=k^2 (exp(-ikx)) ,wobei
L der Laplaceoperator ist und ich diese ganzen nervigen Konstanten weggelassen habe? |
Weiß nicht, ob ich Deine Frage richtig verstehe. Die allgemeine Lösung der freien SG ist ja eine Überlagerunge obiger Ausdrücke über alle k, da gibt es kein diskretes Energiespektrum - letztlich weil es auch kein gebundenes Potenzial gibt.
EDIT: Sollte vielleicht noch darauf hinweisen, daß die echte ("unendliche") ebene Welle natürlich unphysikalisch ist, weil die ja in der Realität von irgendwas abgestrahlt werden muß, und das geschieht immer in begrenzten Wellenpaketen. Aber das ist Dir offensichtlich ja sowieso klar.
_________________
Was ist der Sinn des Lebens? - Keiner, aber Leere ist Fülle für den, der sie sieht.
Zuletzt bearbeitet von step am 29.01.2013, 23:50, insgesamt einmal bearbeitet |
|
| Nach oben |
|
 |
step
registriert

Anmeldungsdatum: 17.07.2003
Beiträge: 22782
Wohnort: Germering
|
 (#1812158) Verfasst am: 29.01.2013, 23:33 Titel: (#1812158) Verfasst am: 29.01.2013, 23:33 Titel: |
 |
|
| petringer hat folgendes geschrieben: | Ich habe jetzt ein Gegenbeispiel für meine ursprüngliche Behauptung gefunden. Man muss einfach nur eine Funktion nehmen, die bei jeder natürlichen Zahl n auf eins geht, der Höcker darf aber nicht breiter als 1/n^2 sein. Dann kann man das Integral mit Summe(1/n^2)=pi^2/6 dominieren.
Was das jetzt physikalisch für einen Sinn hat, weiß ich aber auch nicht. |
Du kannst ja mal versuchen, ein Potenzial V(x) zu finden, so daß die 1-dim. SG genau die von Dir angegebene Lösung hat, oder vielleicht wenigstens
phi²(x) ~ sin²(x) * exp(-n² (x - n*Pi)²)
Das Potenzial sieht aber sicher recht exotisch aus! 
_________________
Was ist der Sinn des Lebens? - Keiner, aber Leere ist Fülle für den, der sie sieht.
|
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1813156) Verfasst am: 01.02.2013, 18:06 Titel: (#1813156) Verfasst am: 01.02.2013, 18:06 Titel: |
 |
|
Meine Bemerkung zu den ebenen Wellen habe ich nur gemacht, weil ich eine ähnliche Argumentation mal irgendwo gelesen habe, dass das Spektrum von freien Teilchen (muss ja kein Licht sein - kann man Licht überhaupt mit der QM beschreiben?) eben von 0 bis unendlich geht.
Klar ist das nicht physikalisch, aber ist es ja nicht sowieso irgendwie unphysikalisch, die Schrödingergleichung über der unendlichen Achse der reellen Zahlen zu lösen?
Als Philosoph (oder zumindest Stammtischphilosoph) interessiere ich mich natürlich auch für die verschiedenen Interpretationen. Habt ihr schon mal was von der Bohmschen Mechanik gehört? Soweit ich ihren Stellenwert beurteilen kann, beweist sie doch, dass aus den Postulaten der QM nicht notwendigerweise Indeterminismus folgen muss.
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
Tso Wang
Vergiß es

Anmeldungsdatum: 21.09.2003
Beiträge: 1433
|
|
| Nach oben |
|
 |
Tso Wang
Vergiß es

Anmeldungsdatum: 21.09.2003
Beiträge: 1433
|
 (#1813184) Verfasst am: 01.02.2013, 19:30 Titel: (#1813184) Verfasst am: 01.02.2013, 19:30 Titel: |
 |
|
| petringer hat folgendes geschrieben: |
Klar ist das nicht physikalisch, aber ist es ja nicht sowieso irgendwie unphysikalisch, die Schrödingergleichung über der unendlichen Achse der reellen Zahlen zu lösen?
|
.
Den Übergang in den "klassischen" Bereich würde ich nicht als unphysikalisch bezeichnen wollen. Aber da kann step als Physiker vermutlich mehr zu sagen.
()
_________________
Geh' weiter
|
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1813191) Verfasst am: 01.02.2013, 19:42 Titel: (#1813191) Verfasst am: 01.02.2013, 19:42 Titel: |
 |
|
Worüber ich mir nicht sicher bin, ist, ob man Licht mit der QM beschreiben kann (ich meine damit die Schrödingergleichung in der ein Term der Form 1/Masse vorkommt, was für masseloses Licht ja keinen Sinn ergibt.) - daher meine Frage. Dass Licht gequantelt ist, weiß ich noch (mehr oder weniger dunkel  ) aus dem Physikunterricht - Photoeffekt. ) aus dem Physikunterricht - Photoeffekt.
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
Tso Wang
Vergiß es

Anmeldungsdatum: 21.09.2003
Beiträge: 1433
|
 (#1813247) Verfasst am: 01.02.2013, 21:07 Titel: (#1813247) Verfasst am: 01.02.2013, 21:07 Titel: |
 |
|
| petringer hat folgendes geschrieben: |
Worüber ich mir nicht sicher bin, ist, ob man Licht mit der QM beschreiben kann (ich meine damit die Schrödingergleichung in der ein Term der Form 1/Masse vorkommt, was für masseloses Licht ja keinen Sinn ergibt.) - daher meine Frage. Dass Licht gequantelt ist, weiß ich noch (mehr oder weniger dunkel  ) aus dem Physikunterricht - Photoeffekt. ) aus dem Physikunterricht - Photoeffekt. |
.
Die Gleichungen der EMW können durch die Maxwellschen Gleichungen hergeleitet und beschrieben werden
http://de.wikipedia.org/wiki/Elektromagnetische_Welle#Herleitung_der_elektromagnetischen_Wellengleichung
Aber sicherlich kann man EMW/Photonen - je nach Versuchsanordnung - ebenfalls eine statistische Wahrscheinlichkeitswelle (Psi-Funktion) zuordnen. Siehe Max Born:
http://www.leifiphysik.de/web_ph11_g8/grundwissen/07stat_deutung/statist_deutung_qm.htm
Bei einem einzelnen Photon und einer einzigen Messung sieht diese Funktion allerdings vermutlich anders aus als bei einer Messung mit vielen Photonen. Aber - wie gesagt - da kann Dir step bestimmt detaillierter weiterhelfen.
()
_________________
Geh' weiter
|
|
| Nach oben |
|
 |
step
registriert

Anmeldungsdatum: 17.07.2003
Beiträge: 22782
Wohnort: Germering
|
 (#1813277) Verfasst am: 01.02.2013, 23:42 Titel: (#1813277) Verfasst am: 01.02.2013, 23:42 Titel: |
 |
|
| petringer hat folgendes geschrieben: | | Worüber ich mir nicht sicher bin, ist, ob man Licht mit der QM beschreiben kann (ich meine damit die Schrödingergleichung in der ein Term der Form 1/Masse vorkommt, was für masseloses Licht ja keinen Sinn ergibt.) - daher meine Frage. |
Nö, in der SG kommt i.a. kein Term 1/m vor. Wenn Du in bestimmten Formen der SG einen Term 1/2m siehst, dann kommt der daher, daß de Hamiltonian einen Term für die kinetische Energie eines Punktteilchens (so etwas wie E = p²/2m) enthält. In der allgemeinen SG steht aber der allgemeine Hamiltonian mit der allgemeinen Energie, die für masselose Objekte kein 1/m enthält.
_________________
Was ist der Sinn des Lebens? - Keiner, aber Leere ist Fülle für den, der sie sieht.
|
|
| Nach oben |
|
 |
Tso Wang
Vergiß es

Anmeldungsdatum: 21.09.2003
Beiträge: 1433
|
 (#1813286) Verfasst am: 02.02.2013, 00:09 Titel: (#1813286) Verfasst am: 02.02.2013, 00:09 Titel: |
 |
|
| step hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | Worüber ich mir nicht sicher bin, ist, ob man Licht mit der QM beschreiben kann (ich meine damit die Schrödingergleichung in der ein Term der Form 1/Masse vorkommt, was für masseloses Licht ja keinen Sinn ergibt.) - daher meine Frage. |
Nö, in der SG kommt i.a. kein Term 1/m vor. Wenn Du in bestimmten Formen der SG einen Term 1/2m siehst, dann kommt der daher, daß de Hamiltonian einen Term für die kinetische Energie eines Punktteilchens (so etwas wie E = p²/2m) enthält. In der allgemeinen SG steht aber der allgemeine Hamiltonian mit der allgemeinen Energie, die für masselose Objekte kein 1/m enthält. |
.
Vielleicht meint er so etwas wie die "freie Schrödinger-Gleichung" (Schnellansicht eines PDF-Links) S. 19, unter 2.21 ....?
Aber die gilt nur für massereiche Teilchen (wie Du ja bereits sagtest).
()
_________________
Geh' weiter
|
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1813305) Verfasst am: 02.02.2013, 01:53 Titel: (#1813305) Verfasst am: 02.02.2013, 01:53 Titel: |
 |
|
Ich sehe jetzt ein, dass der Term 1/m nur vorkommt, wenn man die kinetische Energie gleich p^2/2m setzt, was nicht notwendig ist - danke dafür.
Wie sieht dann der Hamiltonian eines Photons aus? Benutzt man E=c*p? Aber ist dann nicht das Problem, dass p in dieser Gleichung nur sinnvoll als skalare Größe ist, man als den absoluten Betrag nehmen muss p=sqrt(px^2+py^2+pz^2)? Identifiziere ich dann aber px^2+py^2+pz^2=-Laplace, was soll dann sqrt(-Laplace) sein?
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
step
registriert

Anmeldungsdatum: 17.07.2003
Beiträge: 22782
Wohnort: Germering
|
 (#1813390) Verfasst am: 02.02.2013, 15:08 Titel: (#1813390) Verfasst am: 02.02.2013, 15:08 Titel: |
 |
|
| petringer hat folgendes geschrieben: | | Wie sieht dann der Hamiltonian eines Photons aus? Benutzt man E=c*p? Aber ist dann nicht das Problem, dass p in dieser Gleichung nur sinnvoll als skalare Größe ist, man als den absoluten Betrag nehmen muss p=sqrt(px^2+py^2+pz^2)? Identifiziere ich dann aber px^2+py^2+pz^2=-Laplace, was soll dann sqrt(-Laplace) sein? |
- ja, man kann E=c*p benutzen, beziehungsweise genaugenommen E²=p²c²
- p ist Vektor, E ist skalar
- in der SG steht also nirgends ein Wurzelterm.
- es ergibt sich die Klein-Gordon Gleichung mit Spezialfall m=0: quabla ψ = 0, die identisch ist mit den quellenlosen Maxwellgleichungen
_________________
Was ist der Sinn des Lebens? - Keiner, aber Leere ist Fülle für den, der sie sieht.
|
|
| Nach oben |
|
 |
Kival
Profeminist Ghost

Anmeldungsdatum: 14.11.2006
Beiträge: 24071
|
 (#1813401) Verfasst am: 02.02.2013, 15:24 Titel: (#1813401) Verfasst am: 02.02.2013, 15:24 Titel: |
 |
|
| step hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | Wie sieht dann der Hamiltonian eines Photons aus? Benutzt man E=c*p? Aber ist dann nicht das Problem, dass p in dieser Gleichung nur sinnvoll als skalare Größe ist, man als den absoluten Betrag nehmen muss p=sqrt(px^2+py^2+pz^2)? Identifiziere ich dann aber px^2+py^2+pz^2=-Laplace, was soll dann sqrt(-Laplace) sein? |
- ja, man kann E=c*p benutzen, beziehungsweise genaugenommen E²=p²c²
- p ist Vektor, E ist skalar |
Etwas außen vor, verwundert mich aber gerne mal bei physikalischen Formeln: Was ist mit dem Quadrat des Vektors hier gemeint? Skalarprodukt mit sich selbst? Und c ist einfach die skalara Konstante der Lichtgeschwindigkeit?
_________________
"A basic literacy in statistics will one day be as necessary for efficient citizenship as the ability to read and write." (angeblich H. G. Wells)
|
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1813402) Verfasst am: 02.02.2013, 15:25 Titel: (#1813402) Verfasst am: 02.02.2013, 15:25 Titel: |
 |
|
| step hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | Wie sieht dann der Hamiltonian eines Photons aus? Benutzt man E=c*p? Aber ist dann nicht das Problem, dass p in dieser Gleichung nur sinnvoll als skalare Größe ist, man als den absoluten Betrag nehmen muss p=sqrt(px^2+py^2+pz^2)? Identifiziere ich dann aber px^2+py^2+pz^2=-Laplace, was soll dann sqrt(-Laplace) sein? |
- ja, man kann E=c*p benutzen, beziehungsweise genaugenommen E²=p²c²
- p ist Vektor, E ist skalar
- in der SG steht also nirgends ein Wurzelterm.
- es ergibt sich die Klein-Gordon Gleichung mit Spezialfall m=0: quabla ψ = 0, die identisch ist mit den quellenlosen Maxwellgleichungen |
Okay, also dadurch, dass man die Schrödingergleichung auf beiden Seiten quadriert, umgeht man das Problem, dass p strenggenommen ein Wurzelterm wäre, was keinen Sinn hätte. Und dann ergeben sich die klassischen Maxwellgleichungen - nicht schlecht 
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
Kival
Profeminist Ghost

Anmeldungsdatum: 14.11.2006
Beiträge: 24071
|
 (#1813410) Verfasst am: 02.02.2013, 15:30 Titel: (#1813410) Verfasst am: 02.02.2013, 15:30 Titel: |
 |
|
| petringer hat folgendes geschrieben: | | step hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | Wie sieht dann der Hamiltonian eines Photons aus? Benutzt man E=c*p? Aber ist dann nicht das Problem, dass p in dieser Gleichung nur sinnvoll als skalare Größe ist, man als den absoluten Betrag nehmen muss p=sqrt(px^2+py^2+pz^2)? Identifiziere ich dann aber px^2+py^2+pz^2=-Laplace, was soll dann sqrt(-Laplace) sein? |
- ja, man kann E=c*p benutzen, beziehungsweise genaugenommen E²=p²c²
- p ist Vektor, E ist skalar
- in der SG steht also nirgends ein Wurzelterm.
- es ergibt sich die Klein-Gordon Gleichung mit Spezialfall m=0: quabla ψ = 0, die identisch ist mit den quellenlosen Maxwellgleichungen |
Okay, also dadurch, dass man die Schrödingergleichung auf beiden Seiten quadriert, umgeht man das Problem, dass p strenggenommen ein Wurzelterm wäre, was keinen Sinn hätte. Und dann ergeben sich die klassischen Maxwellgleichungen - nicht schlecht  |
Hm, weiß nicht, das ist ja nichtmal ein Trick, zumindest wenn ich das richttig verstehe. Die Energie-Impulsgleichung ist ja eigentlich schon im Kern quadratisch:
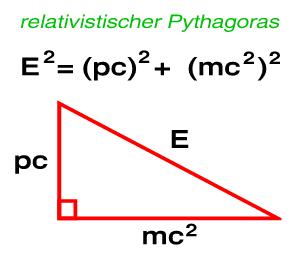
E²=(pc)²+(m*c²)²
m=0 ist ja nur der Sonderfall davon.
_________________
"A basic literacy in statistics will one day be as necessary for efficient citizenship as the ability to read and write." (angeblich H. G. Wells)
|
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1813412) Verfasst am: 02.02.2013, 15:32 Titel: (#1813412) Verfasst am: 02.02.2013, 15:32 Titel: |
 |
|
| Kival hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | step hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | Wie sieht dann der Hamiltonian eines Photons aus? Benutzt man E=c*p? Aber ist dann nicht das Problem, dass p in dieser Gleichung nur sinnvoll als skalare Größe ist, man als den absoluten Betrag nehmen muss p=sqrt(px^2+py^2+pz^2)? Identifiziere ich dann aber px^2+py^2+pz^2=-Laplace, was soll dann sqrt(-Laplace) sein? |
- ja, man kann E=c*p benutzen, beziehungsweise genaugenommen E²=p²c²
- p ist Vektor, E ist skalar
- in der SG steht also nirgends ein Wurzelterm.
- es ergibt sich die Klein-Gordon Gleichung mit Spezialfall m=0: quabla ψ = 0, die identisch ist mit den quellenlosen Maxwellgleichungen |
Okay, also dadurch, dass man die Schrödingergleichung auf beiden Seiten quadriert, umgeht man das Problem, dass p strenggenommen ein Wurzelterm wäre, was keinen Sinn hätte. Und dann ergeben sich die klassischen Maxwellgleichungen - nicht schlecht  |
Hm, weiß nicht, das ist ja nichtmal ein Trick, zumindest wenn ich das richttig verstehe. Die Energie-Impulsgleichung ist ja eigentlich schon im Kern quadratisch:
E²=(pc)²+(m*c²)²
m=0 ist ja nur der Sonderfall davon. |
I see. Ich bin nur gedanklich von der Schrödingergleichung ausgegangen, die eben nicht-quadratisch in der Energie ist.
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
Kival
Profeminist Ghost

Anmeldungsdatum: 14.11.2006
Beiträge: 24071
|
 (#1813417) Verfasst am: 02.02.2013, 15:35 Titel: (#1813417) Verfasst am: 02.02.2013, 15:35 Titel: |
 |
|
Meine rudimentären Physikkenntnisse sind eher relativistisch als quantemechanisch geprägt. Daher von mir halt eher von dort aus.
_________________
"A basic literacy in statistics will one day be as necessary for efficient citizenship as the ability to read and write." (angeblich H. G. Wells)
|
|
| Nach oben |
|
 |
Tso Wang
Vergiß es

Anmeldungsdatum: 21.09.2003
Beiträge: 1433
|
 (#1813418) Verfasst am: 02.02.2013, 15:36 Titel: (#1813418) Verfasst am: 02.02.2013, 15:36 Titel: |
 |
|
| Kival hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | step hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | Wie sieht dann der Hamiltonian eines Photons aus? Benutzt man E=c*p? Aber ist dann nicht das Problem, dass p in dieser Gleichung nur sinnvoll als skalare Größe ist, man als den absoluten Betrag nehmen muss p=sqrt(px^2+py^2+pz^2)? Identifiziere ich dann aber px^2+py^2+pz^2=-Laplace, was soll dann sqrt(-Laplace) sein? |
- ja, man kann E=c*p benutzen, beziehungsweise genaugenommen E²=p²c²
- p ist Vektor, E ist skalar
- in der SG steht also nirgends ein Wurzelterm.
- es ergibt sich die Klein-Gordon Gleichung mit Spezialfall m=0: quabla ψ = 0, die identisch ist mit den quellenlosen Maxwellgleichungen |
Okay, also dadurch, dass man die Schrödingergleichung auf beiden Seiten quadriert, umgeht man das Problem, dass p strenggenommen ein Wurzelterm wäre, was keinen Sinn hätte. Und dann ergeben sich die klassischen Maxwellgleichungen - nicht schlecht  |
Hm, weiß nicht, das ist ja nichtmal ein Trick, zumindest wenn ich das richttig verstehe. Die Energie-Impulsgleichung ist ja eigentlich schon im Kern quadratisch:
E²=(pc)²+(m*c²)²
m=0 ist ja nur der Sonderfall davon. |
.
Genau.
()
_________________
Geh' weiter
|
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1813421) Verfasst am: 02.02.2013, 15:40 Titel: (#1813421) Verfasst am: 02.02.2013, 15:40 Titel: |
 |
|
| Tso Wang hat folgendes geschrieben: | | Kival hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | step hat folgendes geschrieben: | | petringer hat folgendes geschrieben: | | Wie sieht dann der Hamiltonian eines Photons aus? Benutzt man E=c*p? Aber ist dann nicht das Problem, dass p in dieser Gleichung nur sinnvoll als skalare Größe ist, man als den absoluten Betrag nehmen muss p=sqrt(px^2+py^2+pz^2)? Identifiziere ich dann aber px^2+py^2+pz^2=-Laplace, was soll dann sqrt(-Laplace) sein? |
- ja, man kann E=c*p benutzen, beziehungsweise genaugenommen E²=p²c²
- p ist Vektor, E ist skalar
- in der SG steht also nirgends ein Wurzelterm.
- es ergibt sich die Klein-Gordon Gleichung mit Spezialfall m=0: quabla ψ = 0, die identisch ist mit den quellenlosen Maxwellgleichungen |
Okay, also dadurch, dass man die Schrödingergleichung auf beiden Seiten quadriert, umgeht man das Problem, dass p strenggenommen ein Wurzelterm wäre, was keinen Sinn hätte. Und dann ergeben sich die klassischen Maxwellgleichungen - nicht schlecht  |
Hm, weiß nicht, das ist ja nichtmal ein Trick, zumindest wenn ich das richttig verstehe. Die Energie-Impulsgleichung ist ja eigentlich schon im Kern quadratisch:
E²=(pc)²+(m*c²)²
m=0 ist ja nur der Sonderfall davon. |
.
Genau.

() |
Aber dann wäre es doch eigentlich doch gleich besser, wenn man die Schrödingergleichung quadratisch formulieren würde?!
Eine Frage noch: wo würde in der relativistischen Energie-Impuls-Beziehung die potentielle Energie V stehen? (E+V)^2=p^2c^2+(m*c^2)^2 ?
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
Kival
Profeminist Ghost

Anmeldungsdatum: 14.11.2006
Beiträge: 24071
|
 (#1813424) Verfasst am: 02.02.2013, 15:42 Titel: (#1813424) Verfasst am: 02.02.2013, 15:42 Titel: |
 |
|
Schrödinger ist ja eigentlich nicht relativistisch. Man kann es nur anpassen.
_________________
"A basic literacy in statistics will one day be as necessary for efficient citizenship as the ability to read and write." (angeblich H. G. Wells)
|
|
| Nach oben |
|
 |
Tso Wang
Vergiß es

Anmeldungsdatum: 21.09.2003
Beiträge: 1433
|
 (#1813428) Verfasst am: 02.02.2013, 15:46 Titel: (#1813428) Verfasst am: 02.02.2013, 15:46 Titel: |
 |
|
| petringer hat folgendes geschrieben: | Ich sehe jetzt ein, dass der Term 1/m nur vorkommt, wenn man die kinetische Energie gleich p^2/2m setzt, was nicht notwendig ist - danke dafür.
Wie sieht dann der Hamiltonian eines Photons aus? |
.
Taucht der nicht auch im sog. totalen Hamiltonoperator auf ?
Google-Books (Walter Greiner, "Theoretische Physik, Quantentheorie, Band 4, Teil 1")
da wird's allerdings zu (zeitintensiv) mathematisch für mich 
Du sprachst weiter oben von In-/Determinismus. Ich habe an anderer Stelle mal zwei sehr interessante Vorträge zu diesem Thema von John D. Norton (Chemieingenieur und Wissenschaftsphilosoph) verlinkt. Vielleicht interessieren sie Dich mit Deinem philosophischen Hintergrund ja ebenfalls:
Causation : http://lecture2go.uni-hamburg.de/veranstaltungen/-/v/11197
Idealisation, Indeterminism...: http://lecture2go.uni-hamburg.de/veranstaltungen/-/v/11198;jsessionid=5170662207F36EBB14EF7760F6E498F6 (Ton ist am Anfang etwas schlecht-->Mikro)
()
_________________
Geh' weiter
Zuletzt bearbeitet von Tso Wang am 02.02.2013, 15:48, insgesamt einmal bearbeitet |
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1813429) Verfasst am: 02.02.2013, 15:47 Titel: (#1813429) Verfasst am: 02.02.2013, 15:47 Titel: |
 |
|
| Kival hat folgendes geschrieben: | | Schrödinger ist ja eigentlich nicht relativistisch. Man kann es nur anpassen. |
Sorry für meine Verwirrung. Also die Schrödingergleichung ist nichtrelativistisch, aber wenn man sie quadriert und die relativistische Energie-Impuls-Beziehung für E² einsetzt, dann ist sie relativistisch?
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
Zuletzt bearbeitet von petringer am 02.02.2013, 15:49, insgesamt einmal bearbeitet |
|
| Nach oben |
|
 |
petringer
registrierter User
Anmeldungsdatum: 25.01.2013
Beiträge: 24
|
 (#1813433) Verfasst am: 02.02.2013, 15:48 Titel: (#1813433) Verfasst am: 02.02.2013, 15:48 Titel: |
 |
|
Cool, danke. Ich werde sie mir bei Gelegenheit auf jeden Fall reinziehen.
Das Physikbuch ist wirklich derber Stoff, das muss ich mir mal anschauen, wenn ich mal zwei freie Jahre vor mir habe  Ich habe meinen Einstieg übrigens mit Griffiths "Introduction to Quantum Mechanics" versucht. Ich habe meinen Einstieg übrigens mit Griffiths "Introduction to Quantum Mechanics" versucht.
_________________
A-braham sieht B-braham, doch wollte er ein C-braham.
|
|
| Nach oben |
|
 |
|

