| Vorheriges Thema anzeigen :: Nächstes Thema anzeigen |
| Autor |
Nachricht |
Nergal
dauerhaft gesperrt
Anmeldungsdatum: 17.07.2003
Beiträge: 11433
|
 (#323552) Verfasst am: 07.08.2005, 07:52 Titel: Dreiteilung eines Winkels (#323552) Verfasst am: 07.08.2005, 07:52 Titel: Dreiteilung eines Winkels |
 |
|
Dies soll ja mit Lineal und Zirkel nicht möglich sein.
Wieso eigentlich?
Was sind die genauen Voraussetzungen?
|
|
| Nach oben |
|
 |
Lamarck
Radikaler Konstruktivist

Anmeldungsdatum: 28.03.2004
Beiträge: 2148
Wohnort: Frankfurt am Main
|
 (#323554) Verfasst am: 07.08.2005, 09:21 Titel: Re: Dreiteilung eines Winkels (#323554) Verfasst am: 07.08.2005, 09:21 Titel: Re: Dreiteilung eines Winkels |
 |
|
Hi Nergal!
| Nergal hat folgendes geschrieben: | Dies soll ja mit Lineal und Zirkel nicht möglich sein.
Wieso eigentlich?
Was sind die genauen Voraussetzungen? |
Die "Dreiteilung eines Winkels" mittels Lineal und Zirkel ist nur in Sonderfällen möglich. Die hier relevante kubische Gleichung x³ - 3x - 2a = 0 ist eine Gleichung 3. Grades, die im Allgemeinen nicht auf eine quadratische Gleichung reduziert werden kann. Wie im folgenden zu sehen ist, kommst Du hier bei der Bestimmung von x mit der transzendenten Kreiszahl π ins Gehege:
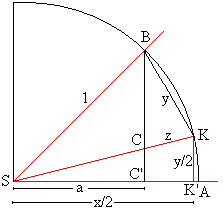
Die Konstruktionsanleitungen für 90, 60 und 30°-Winkel kannst Du beispielsweise bei Wikipedia nachlesen: Winkel_(Geometrie)
Cheers,
Lamarck
_________________
„Nothing in Biology makes sense, except in the light of evolution.” (Theodosius Dobzhansky)
„If you can’t stand algebra, keep out of evolutionary biology.” (John Maynard Smith)
„Computers are to biology what mathematics is to physics.” (Harold Morowitz)
|
|
| Nach oben |
|
 |
Nergal
dauerhaft gesperrt
Anmeldungsdatum: 17.07.2003
Beiträge: 11433
|
 (#323556) Verfasst am: 07.08.2005, 09:45 Titel: (#323556) Verfasst am: 07.08.2005, 09:45 Titel: |
 |
|
Hm, wenn man das Problem nun umgeht dh den Umfang abrollt und die Entststandene Linie 3teilt?
Wieder zurück dürfte schwer werden, vermutlich gilt das dann nicht, oder?
|
|
| Nach oben |
|
 |
Shadaik
evolviert

Anmeldungsdatum: 17.07.2003
Beiträge: 26377
Wohnort: MG
|
 (#323665) Verfasst am: 07.08.2005, 14:44 Titel: (#323665) Verfasst am: 07.08.2005, 14:44 Titel: |
 |
|
Was genau ist die Dreiteilung eines Winkels und wieso kann ich dafür nicht einfach eine Schere nehmen?
_________________
Fische schwimmen nur in zwei Situationen mit dem Strom: Auf der Flucht und im Tode
|
|
| Nach oben |
|
 |
esme
lebt ohne schützende Gänsefüßchen.
Anmeldungsdatum: 12.06.2005
Beiträge: 5667
|
 (#327427) Verfasst am: 14.08.2005, 23:04 Titel: (#327427) Verfasst am: 14.08.2005, 23:04 Titel: |
 |
|
"Mit Zirkel und Lineal" bedeutet, dass durch zwei bereits bekannte Punkte eine Gerade gezogen werden kann, und um einen bereits bekannten Punkt ein Kreis mit einem bereits bekannten Radius gelegt werden kann. Das entspricht dem Lösen von quadratischen Gleichungen, während das Dreiteilen z.B vom Winkel mit 60 Grad dem Lösen einer kubischen Gleichung entspricht, das hat aber mit Pi nichts zu tun.
Die alten Griechen haben praktisch ihr gesamtes mathematisches Wissen als geometrische Konstruktionen formuliert und Konstruktionen mit Zirkel und Lineal haben sie besonders interessiert, aber schon damals waren Konstruktionen zur Dreiteilung des Winkels bekannt, nur eben mit mehr Hilfsmitteln. Das Beeindruckende ist eben, dass es erst 2000 Jahre später möglich war, zu beweisen, dass es wirklich unmöglich war.
Eine Konstruktion zur Winkeldreiteilung ist zum Beispiel möglich mit Zirkel und Lineal, wenn man Markierungen auf das Lineal malen darf.
|
|
| Nach oben |
|
 |
matthias
Gefährder

Anmeldungsdatum: 10.05.2005
Beiträge: 1386
Wohnort: Rechts der Böhme
|
 (#327508) Verfasst am: 15.08.2005, 00:24 Titel: (#327508) Verfasst am: 15.08.2005, 00:24 Titel: |
 |
|
Ich versuch's mal:
Voraussetzung: Es ist eine Menge M von Punkten in der x-y-Ebene (Ebene der komplexen Zahlen) gegeben.
Konstruktion mit Zirkel und Lineal heißt: Mit dem Lineal kann ein Geradenabschnitt durch zwei Punkte gezogen werden (keine Meßfunktion), mit dem Zirkel kann eine Strecke zwischen zwei Punkten abgenommen werden und ein Kreisbogen mit dieser Streckenlänge als Radius um einen dritten Punkt gezogen werden.
Klassisches Konstruktionsproblem: Welche Punktmenge (Schnittpunkte zweier Geraden, zweier Kreislinien, oder einer Geraden und einer Kreislinie) kann aus der Menge M = {(0,0), (1,0)} mit Zirkel und Lineal konstruiert werden?
Jetzt kommt die Algebra ins Spiel: Alle Punkte werden als komplexe Zahlen z = x + iy (i imaginäre Einheit) interpretiert, und die geometrischen Operationen werden in algebraische übersetzt. Das Ergebnis: Die aus M mit Zirkel und Lineal konstruierbaren Punkte bilden einen Teilkörper K der komplexen Zahlen, der unter Quadratwurzelbildung abgeschlossen ist.
Was heißt das? K ist eine Teilmenge der komplexen Zahlen, für die gilt:
(i) 0 = 0 + i0, 1 = 1 + i0 liegen in K
(ii) a in K => -a in K (das Negative von a liegt in K)
(iii) a =/= 0 in K => 1/a in K (der Kehrwert von a liegt in K)
(iv) a, b in K => a + b in K
(v) a, b in K => ab in K
(vi) a in K => Quadratwurzeln aus a liegen in K
Warum Quadratwurzeln? Das liegt daran, daß sich die oben angegebenen Schnittprobleme entweder auf eine lineare oder eine quadratische Gleichung zurückführen lassen.
Wann ist jetzt eine beliebige komplexe Zahl z mit Zirkel und Lineal aus M konstruierbar? Wir definieren K* als den (eindeutig bestimmten!) kleinsten Teilkörper der komplexen Zahlen, der z enthält. Für K* gelten also die Gesetze (i)-(v), und z liegt in K*. Notwendigerweise liegen alle rationalen Zahlen Q in K* (weil 0 und 1 darin enthalten sind).
Eine Maßzahl, der sogenannte Index |K*:Q|, der den Grad angibt, um den sich K* von Q unterscheidet, hilft uns bei der Entscheidung zu sagen, ob z konstruierbar ist.
(Für Experten: |K*:Q| ist gleich der Dimension des Vektorraums K* über dem Körper Q.)
Es gilt der
Satz: z mit Zirkel und Lineal aus M konstruierbar => |K*:Q| ist einer 2er-Potenz
Ohne das jetzt vorzurechnen, kommt man z. B. bei der Frage nach der Dreiteilung des Winkels 60° auf eine Zahl z, die konstruierbar sein müßte, für die jedoch |K*:Q| = 3 gilt. Man kann also die Dreiteilungsfrage mit einem einzigen Gegenbeispiel (negativ) beantworten.
Bemerkung: Für z=π (Pi) ist |K*:Q| Unendlich, weswegen die Quadratur des Kreises mit Zirkel und Lineal nicht möglich ist.
Matthias
_________________
2008 – Jahr der Mathematik
|
|
| Nach oben |
|
 |
Holly Blue
auf eigenen Wunsch deaktiviert
Anmeldungsdatum: 15.02.2005
Beiträge: 2684
|
 (#327849) Verfasst am: 15.08.2005, 18:46 Titel: (#327849) Verfasst am: 15.08.2005, 18:46 Titel: |
 |
|
Hä   
Bahnhof......
|
|
| Nach oben |
|
 |
matthias
Gefährder

Anmeldungsdatum: 10.05.2005
Beiträge: 1386
Wohnort: Rechts der Böhme
|
 (#327851) Verfasst am: 15.08.2005, 18:50 Titel: (#327851) Verfasst am: 15.08.2005, 18:50 Titel: |
 |
|
| Holly Blue hat folgendes geschrieben: | Hä   
Bahnhof...... |
Welcher Teil ist Dir unklar 
_________________
2008 – Jahr der Mathematik
|
|
| Nach oben |
|
 |
lemonstar
registrierter User
Anmeldungsdatum: 17.07.2003
Beiträge: 1004
|
 (#327886) Verfasst am: 15.08.2005, 20:17 Titel: (#327886) Verfasst am: 15.08.2005, 20:17 Titel: |
 |
|
| matthias hat folgendes geschrieben: | | Holly Blue hat folgendes geschrieben: | Hä :?: :?: :?:
Bahnhof...... |
Welcher Teil ist Dir unklar :?: |
Umgekehrt gefragt wär wohl sinnvoller ;-)
_________________
eindrucksvolles
|
|
| Nach oben |
|
 |
matthias
Gefährder

Anmeldungsdatum: 10.05.2005
Beiträge: 1386
Wohnort: Rechts der Böhme
|
 (#327917) Verfasst am: 15.08.2005, 21:15 Titel: (#327917) Verfasst am: 15.08.2005, 21:15 Titel: |
 |
|
| lemonstar hat folgendes geschrieben: | Umgekehrt gefragt wär wohl sinnvoller  |
Ich befürchte es auch. Deswegen
@Holly Blue
Mal ein ganz ernsthaftes Angebot: Was hältst Du von einem Kurs
Winkeldreiteilung für Laien erklärt ?
Inhalt: Im Kurs wird das schon aus der Antike überlieferte mathematische Problem "Dreiteilung eines Winkels" behandelt. Ausgehend von der geometrischen Anschauung werden die theoretischen Methoden entwickelt, die zur Beschreibung und Lösung des Problems erforderlich sind. Die algebraischen Mittel werden auf elementare Weise hergeleitet, und nur insoweit, wie sie zur Lösungsfindung beitragen. Der Kurs schließt mit dem Beweis der Unmöglichkeit der Winkeldreiteilung im allgemeinen Fall ab.
Vorkenntnisse: Mathematik 10. Klasse Gymnasium (nicht allzu große Lücken können ausgefüllt werden).
Aufbau: Der Kurs gliedert sich in einander abwechselnde Vorträge des Dozenten und Übungsaufgaben, die von der Kursteilnehmerin schriftlich zu bearbeiten sind. Die Lösungen der Übungsaufgaben werden ausführlich besprochen, Hilfestellung zur Lösung wird -- soweit möglich und nötig -- geleistet.
Ort: freigeisterhaus.de
Zeit: nach Vereinbarung (d. h. ohne feste Vorgaben, ohne Zeitdruck, nach Bedarf)
Meine Leistungen:
- mathematisch fundierte Erklärung des Problems der Winkeldreiteilung mit Übungen
- Bewußtseinserweiterung ohne Drogen und ohne komplizierte oder ethisch nicht vertretbare körperliche Experimente
- Begleitung als Tutor (auch über PN) und Übungsleiter
Deine Leistungen:
- regelmäßige Anwesenheit
- Anfertigung von Lösungen zu den Übungsaufgaben
Kursmaterialien: Weißes Papier, Bleistift, Zirkel und Lineal, Internetzugang.
Am Ende des Kurses wird der Teilnehmerin bei erfolgreichem Abschluß ein Z e r t i f i k a t ausgestellt.
Matthias
P.S.: Sollte sich Holly Blue unpäßlich fühlen, kann natürlich auch jemand anderes die Rolle des interessierten Laien übernehmen. 
_________________
2008 – Jahr der Mathematik
|
|
| Nach oben |
|
 |
Lamarck
Radikaler Konstruktivist

Anmeldungsdatum: 28.03.2004
Beiträge: 2148
Wohnort: Frankfurt am Main
|
 (#328037) Verfasst am: 16.08.2005, 00:30 Titel: (#328037) Verfasst am: 16.08.2005, 00:30 Titel: |
 |
|
Hi Trisektierer!
| matthias hat folgendes geschrieben: | | Ohne das jetzt vorzurechnen, kommt man z. B. bei der Frage nach der Dreiteilung des Winkels 60° auf eine Zahl z, die konstruierbar sein müßte, [...]. |
Wie jetzt? 
Cheers,
Lamarck
_________________
„Nothing in Biology makes sense, except in the light of evolution.” (Theodosius Dobzhansky)
„If you can’t stand algebra, keep out of evolutionary biology.” (John Maynard Smith)
„Computers are to biology what mathematics is to physics.” (Harold Morowitz)
|
|
| Nach oben |
|
 |
Galaxisherrschers Katze
Verwöhntes Haustier

Anmeldungsdatum: 06.04.2005
Beiträge: 5018
|
 (#328042) Verfasst am: 16.08.2005, 00:52 Titel: (#328042) Verfasst am: 16.08.2005, 00:52 Titel: |
 |
|
Was ist daran so schwer? (Oder sollen die Teile etwa gleich groß sein?)
_________________
"(...)steak can be attached to a baby to attract lions(...)" (Aus der ESRB-Beschreibung von Scribblenauts)
|
|
| Nach oben |
|
 |
matthias
Gefährder

Anmeldungsdatum: 10.05.2005
Beiträge: 1386
Wohnort: Rechts der Böhme
|
 (#328045) Verfasst am: 16.08.2005, 00:58 Titel: (#328045) Verfasst am: 16.08.2005, 00:58 Titel: |
 |
|
| Lamarck hat folgendes geschrieben: | Hi Trisektierer!
| matthias hat folgendes geschrieben: | | Ohne das jetzt vorzurechnen, kommt man z. B. bei der Frage nach der Dreiteilung des Winkels 60° auf eine Zahl z, die konstruierbar sein müßte, [...]. |
Wie jetzt?  |
OK: Angenommen, der Winkel 60° wäre mittels Zirkel und Lineal drittelbar, so könnte man leicht eine komplexe Zahl z finden, die man ebenfalls konstruieren könnte (da gäbe es dann mehrere Möglichkeiten, z. B. z = cos 20° + i sin 20° warum?), für die aber |K*:Q|=3 keine 2er-Potenz ist. Zufrieden?
Matthias
_________________
2008 – Jahr der Mathematik
|
|
| Nach oben |
|
 |
göttertod
Atheist und Zweifelsäer

Anmeldungsdatum: 20.08.2004
Beiträge: 1565
Wohnort: Freiburg
|
 (#328050) Verfasst am: 16.08.2005, 01:08 Titel: (#328050) Verfasst am: 16.08.2005, 01:08 Titel: |
 |
|
ich mag das Freigeisterhaus

_________________
auf dass die Bücher von "Iain Banks" Wirklichkeit werden
The Jimmy Dore Show
jede Tradition ist es wert sich an sie zu erinnern, aber nicht jede Tradition ist es wert gelebt zu werden
|
|
| Nach oben |
|
 |
Lamarck
Radikaler Konstruktivist

Anmeldungsdatum: 28.03.2004
Beiträge: 2148
Wohnort: Frankfurt am Main
|
 (#328051) Verfasst am: 16.08.2005, 01:15 Titel: (#328051) Verfasst am: 16.08.2005, 01:15 Titel: |
 |
|
Hi matthias!
| matthias hat folgendes geschrieben: | | OK: Angenommen, der Winkel 60° wäre mittels Zirkel und Lineal drittelbar, so könnte man leicht eine komplexe Zahl z finden, die man ebenfalls konstruieren könnte (da gäbe es dann mehrere Möglichkeiten, z. B. z = cos 20° + i sin 20° warum?), für die aber |K*:Q|=3 keine 2er-Potenz ist. Zufrieden? |
Nein. 
Ein wäre, könnte, gäbe ist nicht hinreichend - offenbar ist es hier nötig, eine Strecke als positive rationale Zahl darzustellen. Aber niemand hat gesagt, dass diese Konstruktion trivial ist.
Cheers,
Lamarck
_________________
„Nothing in Biology makes sense, except in the light of evolution.” (Theodosius Dobzhansky)
„If you can’t stand algebra, keep out of evolutionary biology.” (John Maynard Smith)
„Computers are to biology what mathematics is to physics.” (Harold Morowitz)
|
|
| Nach oben |
|
 |
matthias
Gefährder

Anmeldungsdatum: 10.05.2005
Beiträge: 1386
Wohnort: Rechts der Böhme
|
 (#328052) Verfasst am: 16.08.2005, 01:17 Titel: (#328052) Verfasst am: 16.08.2005, 01:17 Titel: |
 |
|
| Galaxisherrschers Katze hat folgendes geschrieben: | | Was ist daran so schwer? (Oder sollen die Teile etwa gleich groß sein?) |
Ja, sollen sie. Das Problem ist: Gegeben ist ein beliebiger Winkel φ (phi). Gib eine allgemeine Konstruktion an, die den Winkel φ/3 konstruiert.
Wir können annehmen, φ sei durch drei Punkte A, B, C gegeben, also φ = ∠ABC. Aus A = (0,0) und C = (1,0) ist z. B. der Punkt B = (1/2, sqrt(3)/2)* als dritter Punkt in dem gleichseitigen Dreieck ACB konstruierbar. Die Aufgabe lautet jetzt: Konstruiere aus φ = ∠ABC = 60° den Winkel φ/3 = 20°. Du kannst es gerne versuchen  . Du solltest ihn zumindest halbieren können. . Du solltest ihn zumindest halbieren können.
| göttertod hat folgendes geschrieben: | ich mag das Freigeisterhaus
 |
Das tun wir doch alle, oder?
Matthias
____________________
*sqrt = square root = Quadratwurzel
_________________
2008 – Jahr der Mathematik
|
|
| Nach oben |
|
 |
matthias
Gefährder

Anmeldungsdatum: 10.05.2005
Beiträge: 1386
Wohnort: Rechts der Böhme
|
 (#328058) Verfasst am: 16.08.2005, 01:28 Titel: (#328058) Verfasst am: 16.08.2005, 01:28 Titel: |
 |
|
Hi Lamarck!
| Lamarck hat folgendes geschrieben: | Hi matthias!
| matthias hat folgendes geschrieben: | | OK: Angenommen, der Winkel 60° wäre mittels Zirkel und Lineal drittelbar, so könnte man leicht eine komplexe Zahl z finden, die man ebenfalls konstruieren könnte (da gäbe es dann mehrere Möglichkeiten, z. B. z = cos 20° + i sin 20° warum?), für die aber |K*:Q|=3 keine 2er-Potenz ist. Zufrieden? |
Nein. 
Ein wäre, könnte, gäbe ist nicht hinreichend - offenbar ist es hier nötig, eine Strecke als positive rationale Zahl darzustellen. Aber niemand hat gesagt, dass diese Konstruktion trivial ist.
Cheers,
Lamarck |
Ich verstehe Deinen Einwand nicht ganz. Mit wäre, könnte, gäbe will ich hier nur ausdrücken, daß ich von einer Annahme für einen indirekten Beweis ausgehe. Ich nehme also einfach an, es gäbe eine Konstruktion, und erhalte einen Widerspruch zu dem angegeben Satz, dessen Gültigkeit ich einfach ohne Beweis voraussetze.
Matthias
_________________
2008 – Jahr der Mathematik
|
|
| Nach oben |
|
 |
Lamarck
Radikaler Konstruktivist

Anmeldungsdatum: 28.03.2004
Beiträge: 2148
Wohnort: Frankfurt am Main
|
 (#328061) Verfasst am: 16.08.2005, 01:36 Titel: (#328061) Verfasst am: 16.08.2005, 01:36 Titel: |
 |
|
Hi matthias!
| matthias hat folgendes geschrieben: | | Ich verstehe Deinen Einwand nicht ganz. Mit wäre, könnte, gäbe will ich hier nur ausdrücken, daß ich von einer Annahme für einen indirekten Beweis ausgehe. Ich nehme also einfach an, es gäbe eine Konstruktion, und erhalte einen Widerspruch zu dem angegeben Satz, dessen Gültigkeit ich einfach ohne Beweis voraussetze. |
Nun ja, das Problem ist hier doch kurzum: Wie fischt Du die entsprechenden rationalen Zahlen aus den komplexen heraus? Das Original benutzt hierfür einen doppelten indirekten Beweis. Gelingt es also bsw. einen ∠ = 11° zu trisektieren?
Cheers,
Lamarck
_________________
„Nothing in Biology makes sense, except in the light of evolution.” (Theodosius Dobzhansky)
„If you can’t stand algebra, keep out of evolutionary biology.” (John Maynard Smith)
„Computers are to biology what mathematics is to physics.” (Harold Morowitz)
|
|
| Nach oben |
|
 |
IvanDrago
Ösifreund und Pendler zwischen den Welten
Anmeldungsdatum: 18.07.2005
Beiträge: 2876
|
 (#328069) Verfasst am: 16.08.2005, 01:50 Titel: (#328069) Verfasst am: 16.08.2005, 01:50 Titel: |
 |
|
hui... ein mathematisch-geistig völlig überforderter und sich diesbezüglich jenseits eures Wissens befindlicher IvanDrago...
_________________
"Eine Stadt freut sich, wenn's den Gerechten wohlgeht, und wenn die Gottlosen umkommen, wird man froh." Sprüche 11, 10
Heike N. meint: "IvanDrago for President!"
Faszination braucht keine höhere Macht.
Zuletzt bearbeitet von IvanDrago am 16.08.2005, 01:51, insgesamt einmal bearbeitet |
|
| Nach oben |
|
 |
matthias
Gefährder

Anmeldungsdatum: 10.05.2005
Beiträge: 1386
Wohnort: Rechts der Böhme
|
 (#328070) Verfasst am: 16.08.2005, 01:51 Titel: (#328070) Verfasst am: 16.08.2005, 01:51 Titel: |
 |
|
Hi Lamarck!
| Lamarck hat folgendes geschrieben: | | Wie fischt Du die entsprechenden rationalen Zahlen aus den komplexen heraus? |
Rationale Zahlen lassen sich immer konstruieren, da sich Vielfaches und beliebiger n-ter Teil einer Strecke konstruieren lassen.
| Lamarck hat folgendes geschrieben: | | Das Original benutzt hierfür einen doppelten indirekten Beweis. |
Welches Original meinst Du?
| Lamarck hat folgendes geschrieben: | | Gelingt es also bsw. einen ∠ = 11° zu trisektieren? |
Im Moment fehlt mir die Zeit, den Grad der entsprechenden Körpererweiterung zu berechnen. 
Ich sehe auch nicht die direkte Verbindung zur Konstruierbarkeit rationaler Zahlen.
Matthias
_________________
2008 – Jahr der Mathematik
|
|
| Nach oben |
|
 |
Holly Blue
auf eigenen Wunsch deaktiviert
Anmeldungsdatum: 15.02.2005
Beiträge: 2684
|
 (#328145) Verfasst am: 16.08.2005, 08:04 Titel: (#328145) Verfasst am: 16.08.2005, 08:04 Titel: |
 |
|
Huhu!
Also ich bin nur kurz da und hab nicht so viel Zeit, jedenfalls finde ich das schon sehr erstaunlich, dass man sich damit so beschäftigen kann. Ich hab Mathematik nie gemocht und bin auch nicht sonderlich gut drin. Ich wüßte ehrlich gesagt auch nicht, was diese Dreiteilung überhaupt bezwecken soll? Hat man nen 90 Grad Winkel, dann kann man das doch einfach durch 3 teilen, oder bin ich jetzt ganz doof? Also ich weiß nicht.
@matthias
Das ist ein sehr liebes Angebot, allerdings hab ich Semesterferien und daher
a) nicht immer verfügbar, da ich vielleicht auch vorhabe in Urlaub zu gehen
b) hab ich keine große Lust, mich mit Mathe quälen zu lassen
c) die Befürchtung, dass das ganze nichts bringt, weils mich nicht so wirklich interessiert...
Aber trotzdem vielen Dank für das Angebot.
Grüße,
Holly
|
|
| Nach oben |
|
 |
matthias
Gefährder

Anmeldungsdatum: 10.05.2005
Beiträge: 1386
Wohnort: Rechts der Böhme
|
 (#328202) Verfasst am: 16.08.2005, 10:21 Titel: (#328202) Verfasst am: 16.08.2005, 10:21 Titel: |
 |
|
| Holly Blue hat folgendes geschrieben: | Huhu!
Also ich bin nur kurz da und hab nicht so viel Zeit, jedenfalls finde ich das schon sehr erstaunlich, dass man sich damit so beschäftigen kann. Ich hab Mathematik nie gemocht und bin auch nicht sonderlich gut drin. Ich wüßte ehrlich gesagt auch nicht, was diese Dreiteilung überhaupt bezwecken soll? Hat man nen 90 Grad Winkel, dann kann man das doch einfach durch 3 teilen, oder bin ich jetzt ganz doof? Also ich weiß nicht. |
Das Wissen um die Dreiteilung selbst bringt im Grunde gar nichts, das hast Du vollkommen richtig erkannt.  Die historische Frage, ob man bestimmte Punkte in der Ebene konstruieren kann, ist algebraisch gelöst, die Frage, wie man im positiven Falle die Konstruktion tatsächlich durchführt, ist nur von sehr nachrangigem Interesse. Kaum ein Mensch möchte das GAUßsche 17eck konstruieren, vom 257eck gar nicht zu reden. Dennoch hat die Methode der Beweisführung einen wichtigen Stellenwert in der Mathematik und in der Mathematikgeschichte und hat die erfolgreiche Algebraisierung vieler Probleme vorangetrieben. Die historische Frage, ob man bestimmte Punkte in der Ebene konstruieren kann, ist algebraisch gelöst, die Frage, wie man im positiven Falle die Konstruktion tatsächlich durchführt, ist nur von sehr nachrangigem Interesse. Kaum ein Mensch möchte das GAUßsche 17eck konstruieren, vom 257eck gar nicht zu reden. Dennoch hat die Methode der Beweisführung einen wichtigen Stellenwert in der Mathematik und in der Mathematikgeschichte und hat die erfolgreiche Algebraisierung vieler Probleme vorangetrieben.
Du kannst natürlich einen Winkel dem Wert nach durch drei teilen, das Problem ist, ob Du mit Hilfe von Zirkel und Lineal auch diesen gedrittelten Winkel mechanisch konstruieren kannst. Elitäre Dinge wie Winkelmesser und Scheren bleiben natürlich verboten.
| Holly Blue hat folgendes geschrieben: | @matthias
Das ist ein sehr liebes Angebot, allerdings hab ich Semesterferien und daher
a) nicht immer verfügbar, da ich vielleicht auch vorhabe in Urlaub zu gehen
b) hab ich keine große Lust, mich mit Mathe quälen zu lassen
c) die Befürchtung, dass das ganze nichts bringt, weils mich nicht so wirklich interessiert...
Aber trotzdem vielen Dank für das Angebot.
Grüße,
Holly |
zu a) Das wäre auch das Hauptproblem bei mir. Habe zwar keine Semesterferien mehr, kann mich mit dem Thema aber auch nicht immer beschäftigen.
zu b) Du hast also entweder nur eine kleine Lust, oder Du willst Dich nicht mit Mathe quälen lassen oder Dich mit Mathe nicht quälen lassen. 
zu c) Da ich mich selbst auch für viele Sachen herzhaft nicht interessiere, kann ich das gut nachvollziehen.
__________
Das Ganze hätte sowieso einen sehr experimentellen Charakter, Ergebnis ungewiß.
Falls jemand das Thema selbst bearbeiten will, hätte ich noch zwei Buchempfehlungen:
1. Richard Courant, Herbert Robbins, What is Mathematics?, Oxford University Press, ISBN 0195105192 (dt. Was ist Mathematik?, Springer, ISBN 354063777X):
In diesem Buch werden Themen der Algebra, Geometrie und Analysis in elementarer Form behandelt, darunter auch Konstruktionsprobleme mit Zirkel und Lineal. Dem Klappentext der Springer-Ausgabe habe ich nichts hinzuzufügen. Daß Albert Einstein und Herman Weyl das Buch gelobt haben, heißt nicht, daß es von Laien nicht mit Gewinn gelesen werden kann, ganz im Gegenteil.
2. Ernst Kunz, Algebra, Vieweg, ISBN 3528072431 (Neuauflage geplant):
Im Gegensatz zu anderen mir bekannten Algebrabüchern für Mathematikstudenten werden Konstruktionsprobleme hier sehr ausführlich und anschaulich behandelt, ein großer Teil der Theorie in den ersten drei Kapiteln wird ausgehend von diesen Problemen motiviert und entwickelt. Es kann auch von Nichtmathematikern gelesen werden, erfordert aber Kenntnisse in linearer Algebra.
Matthias
_________________
2008 – Jahr der Mathematik
|
|
| Nach oben |
|
 |
Dreiteilung
registrierter User
Anmeldungsdatum: 22.01.2006
Beiträge: 1
Wohnort: Potsdam
|
 (#406332) Verfasst am: 22.01.2006, 15:31 Titel: Die Dreiteilung eines Winkels (#406332) Verfasst am: 22.01.2006, 15:31 Titel: Die Dreiteilung eines Winkels |
 |
|
Im Jahr 2005 ist es dem Potsdamer Autor Karel Markowski gelungen den Beweis anzutreten, dass "Die Dreiteilung eines Winkels" wie von altersher gefordert mit Zirkel und Lineal möglich ist. Er hat darüber im Trigon Verlag Ltd. mit Sitz in Potsdam ein Buch mit der ISBN Nr. 3-9810752-0-X veröffentlicht.
Mit diesem Beweis widerlegt Karel Markowski die angebliche These von Galois aus dem Jahre 1832, dass dieser Beweis nicht möglich ist.
Noch widerstehen die Mathematiker der "Winkelrevolution" aus Potsdam, doch wer sich intensiv mit der Beweisführung von Karel Markowski auseinandersetzt wird ganz schnell zu der Überzeugung kommen, dass seine Beweisführung fehlerfrei und exakt sowie nachvollziehbar ist.
_________________
Die Dreiteilung eines Winkels von Karel Markowski
|
|
| Nach oben |
|
 |
Babyface
Altmeister

Anmeldungsdatum: 17.07.2003
Beiträge: 11519
|
 (#406335) Verfasst am: 22.01.2006, 15:34 Titel: (#406335) Verfasst am: 22.01.2006, 15:34 Titel: |
 |
|
Thread aus Mammiie nach Wissenschaft & Technik verschoben. Bist jetzt freigeschaltet und kannst überall posten.
_________________
posted by Babyface
.
|
|
| Nach oben |
|
 |
Heike J
registrierter User
Anmeldungsdatum: 16.07.2003
Beiträge: 26284
|
 (#406336) Verfasst am: 22.01.2006, 15:35 Titel: (#406336) Verfasst am: 22.01.2006, 15:35 Titel: |
 |
|
| Threads zum gleichen Thema verschmolzen.
|
|
| Nach oben |
|
 |
Maxinquaye
registrierter User

Anmeldungsdatum: 31.03.2004
Beiträge: 40
|
 (#407154) Verfasst am: 24.01.2006, 00:13 Titel: (#407154) Verfasst am: 24.01.2006, 00:13 Titel: |
 |
|
Eine Frage zur Auflösbarkeit algebraischer Gleichungen:
Abel hat doch gezeigt, dass Gleichungen fünften Grades i.a. nicht auflösbar sind. Kennt jemand den Beweis und kann ihn kurz skizzieren? (Ich meine jetzt nicht das Ergebnis von Galois).
_________________
Wir müssen wissen. Wir werden wissen. (D. Hilbert)
|
|
| Nach oben |
|
 |
Othilic
Gast
|
 (#407223) Verfasst am: 24.01.2006, 01:47 Titel: Re: Die Dreiteilung eines Winkels (#407223) Verfasst am: 24.01.2006, 01:47 Titel: Re: Die Dreiteilung eines Winkels |
 |
|
| Dreiteilung hat folgendes geschrieben: | Im Jahr 2005 ist es dem Potsdamer Autor Karel Markowski gelungen den Beweis anzutreten, dass "Die Dreiteilung eines Winkels" wie von altersher gefordert mit Zirkel und Lineal möglich ist. Er hat darüber im Trigon Verlag Ltd. mit Sitz in Potsdam ein Buch mit der ISBN Nr. 3-9810752-0-X veröffentlicht.
Mit diesem Beweis widerlegt Karel Markowski die angebliche These von Galois aus dem Jahre 1832, dass dieser Beweis nicht möglich ist.
Noch widerstehen die Mathematiker der "Winkelrevolution" aus Potsdam, doch wer sich intensiv mit der Beweisführung von Karel Markowski auseinandersetzt wird ganz schnell zu der Überzeugung kommen, dass seine Beweisführung fehlerfrei und exakt sowie nachvollziehbar ist. |
Hat Karel Markowski eine explizite Konstruktion angegeben? Dann hat er keine Chance, Beachtung zu finden. In vielen mathematischen Insituten gibt es Leute, die die sogenannte Laienpost beantworten. Dauerbrenner der Laienpost sind u.a. die abgedrehtesten Anleitungen für Winkeldreiteilungs-konstruktionen. Deren Verfasser fühlen sich alle, alle als verkannte Revolutionäre. Aber in jeder Konstruktion steckt irgendwo ein Fehler. Die Klassiker (Schere benutzt, Lineal markiert... ) sind schnell zu entlarven. Andere Anleitungen sind die Arbeit von Jahren, hochkompliziert, man muss entsprechend viel Zeit aufwenden, um sich überhaupt erst hineinzudenken. Ich denke, die meisten Mathematiker kennen die Laienpost-Ordner, wurden evtl auch mal dazu verdonnert, den Fehler in einer solchen Konstruktion zu finden, und sind einfach nicht bereit, die Zeit und Energie aufzuwenden, sich mit der fünfhundertsten solchen Konstruktion intensiv zu befassen.
Wenn Karel Markowski überzeugt ist, dass er Recht hat, soll er seine Konstruktion doch dazu verwenden, ein Gegenbeispiel zum nur zitierten Satz des Standardbeweis (wie von matthias oben skizziert) zu finden und dadurch den Fehler im Standardbeweis aufdecken, den Zig-tausende von Mathematik-Studenten und Tausende von Professoren nicht gesehen haben. _Das_ wäre eine Revolution, die sofort Beachtung finden würde.
|
|
| Nach oben |
|
 |
sascha
bekennender magnusfe-Fan

Anmeldungsdatum: 30.08.2004
Beiträge: 1449
Wohnort: Bremen
|
 (#407228) Verfasst am: 24.01.2006, 02:11 Titel: (#407228) Verfasst am: 24.01.2006, 02:11 Titel: |
 |
|
| Holly Blue hat folgendes geschrieben: | Hä   
Bahnhof...... |
Dann solltest Du Dir das geniale Buch "Mathematik zum Studienbeginn" von Prof. Arnfried Kemnitz kaufen. Mir ging das in der Schule genau wie Dir, aber heute bin ich durch Programmieren und Naturwissenschaften gezwungen, das zu können. Das Buch ist geeignet, den ganzen Stoff von Klasse 5 bis 12 nachzuholen. "Mathematik zum Studienbeginn", das ist wie Kaffee zum Frühstück.
_________________
"There is no justice, no righteousness in your religions. I awoke from that dream long ago. The reality of this world is that strength rules. Those who aren't willing to push, are simply going to get run over." - Madae
|
|
| Nach oben |
|
 |
|

